the jsomers.net blog.

When I was planning my first long drive from school in Ann Arbor back home to New Jersey, I remember looking up directions on Google Maps and noticing, as in the results here, that it really doesn't take a lot of steps -- or driving maneuvers -- to get what seems to be a pretty long way across the country. In fact it only requires seventeen turns using the route Google gives, and even that number is inflated (those "keep left" and "keep right" steps are helpful, maybe, but not necessary).

Just for fun, I tried comparing that 500+ mile trip to one a fraction of its size, something closer to ten miles. You can see such a route here.

Remarkably, at only 2% of the distance, this short hop from one small town in New Jersey to another requires just fifteen steps, or only two fewer than the hefty road trip to Michigan.

I began to wonder: what's the relationship between the length of a road trip and the complexity of the route? Do most trips, long or short, require roughly the same number of steps? How many steps are there in the most complex route in the country? What's the distribution of step counts for every possible route in the contiguous United States?

These questions turn out to be tractable, thanks in large part to Google's Directions API, which gives lowly developers like me access to their full suite of mapping, geolocation, and pathfinding algorithms, huge stores of data, and fast servers that can deliver tens of thousands of query results to a single client computer in a matter of minutes.

Before we dive into methods and results, though, let's lay out exactly what we're looking for:

1. We want a histogram of step counts for some representative sample of routes within the US. This will give us a really good sense of how complex a typical road trip might be.

2. We'd like to find the most complex route in the country, i.e., a pair of points such that the driving directions between them, given by Google, include a larger number of steps than for any other pair in the contiguous US. It's extremely unlikely that we'll find the monster route, but at least we'd like a ballpark estimate of its step count -- is it 35, 500, 90, 180?

3. We want a plot of route distance against route complexity. What will the plot look like? Is complexity a linear function of distance? Is there a direct or inverse relationship? Will there be any pattern at all?

4. It would be pretty cool to find a "coefficient of friction" for regions in America, that is, a numerical estimate of how hard it is to drive through a particular region based on how many steps there are, on average, in a route passing through it. We could use this information to create a "heat map" of the entire US, with individual counties or zip codes shaded by friction. Such a map would help us figure out which states have the thorniest roads, or where the most straightforward routes are, or which cities are the hardest to get out of.

To get started, then, I went looking for a random sample of points. One way to do that would be to draw a box inscribed within the continental US and simply generate random lat-longs within that box. The trouble with that method, I thought, was that it could easily drop you in barren or ridiculous places like deserts or lakes; I wanted to focus on plausible real-life trips from one population center to another.

So I went looking for a data set, and before long, found one: the "MaxMind World Cities with Population" file, a 33 MB free download with more than enough data to get things rolling: after eliminating non-U.S. cities (a simple grep did the trick, since the text is nicely structured), I was left with 141,989 points covering nearly every corner of the country.

I hacked together a tiny Rails project (RoR being my hammer-that-makes-everything-look-like-a-nail at the moment) to (a) load the cities and lat-longs into some structured form, (b) drop that data into an HTML page hooked up to the JavaScript Google Directions API, and (c) write the results back to a database. All of the relevant code, along with a SQLite3 database with the structured cities data and results, is available at this github project page.

Perhaps the most important snippet, which I'll excerpt below, is the code that actually samples points and talks to Google:

var map;
var directionDisplay;
var directionsService;
var stepDisplay;
var markerArray = [];
var step_counts = [];
var step_summaries = [];

function initialize() {
  // Instantiate a directions service.
  directionsService = new google.maps.DirectionsService();
}

function calcRoute(start, end) {
  // Retrieve the start and end locations and create
  // a DirectionsRequest using DRIVING directions.
  var city_start = [start[2], start[3]].join(", ");
  var city_end = [end[2], end[3]].join(", ");
  var latlong_start = [start[0], start[1]].join(",");
  var latlong_end = [end[0], end[1]].join(",");
  var request = {
      origin: latlong_start,
      destination: latlong_end,
      travelMode: google.maps.DirectionsTravelMode.DRIVING
  };

  // Route the directions and pass the response to a
  // function to count the number of returned steps.
  directionsService.route(request, function(response, status) {
    if (status == google.maps.DirectionsStatus.OK) {
      var step_ct = countSteps(response);
      step_counts.push(step_ct);
      step_summaries.push([step_ct, city_start, city_end])
    } else {
      console.warn("Couldn't count steps for this route.");
    }
  });
}

function countSteps(directionResult) {
    var myRoute = directionResult.routes[0].legs[0];
    return myRoute.steps.length;
}

function getAndExecutePairs(n) {
    $.get("/directions/get_pairs", {n: n},
        function(ret) {
            pairs = ret;
            console.log(n + " lat/long pairs downloaded successfully.");
            execute(pairs);
        }
    )
}

function execute(pairs) {
    for (i = 0; i < pairs.length; i++) {
        pair = pairs[i];
        start = pair[0];
        end = pair[1];
        calcRoute(start, end);
    }
}

It's all pretty straightforward. The process is kicked off by the getAndExecutePairs() function, which just hits the Rails server for n pairs of cities. This is the code it calls:

def get_pairs
  n = params[:n].to_i
  cities = City.find(:all, :limit => n * 2, :order => "random()");
  lat_longs = cities.collect {|c| [c.latitude, c.longitude, c.city, c.state]}
  pairs = Hash[*lat_longs].to_a
  render :json => pairs
end

And that's it. With just ~100 or so lines of code, I was able to get a decent grip on the first three of the four questions posed above. In particular:

1. What's the distribution of step counts for every possible route in the contiguous United States?

The answer, based on a random sample of some 2,000 points (and confirmed later by 8,000 more trials), is that you have a sort of right-skewed distribution centered at 20-30 steps and tailing out near 60.

2. How many steps are there in the most complex route in the country?

This is a lot less definitive, but the answer I got was 69 steps, in a route from Ponderose Pine, NM to Wildwood, MN. A friend suggested something like the following approach for finding more complicated routes:

Suppose you're getting "good" (i.e., stepful) routes between points A and B. Draw a box around each of A and B and "wiggle" your start points within that box. If wiggling in one direction removes steps, try wiggling in another direction; or if it's not direction that matters, but rather something tricky like "being within a development or behind a river," maybe you could just select points within the box randomly and assign scores to different areas (sort of like a game of Battleship). That way you slowly optimize promising routes until you end up with truly high numbers.

One potential pitfall of this approach is that there could be discontinuities -- A to B could take an unremarkable 35 steps, but (A + ε) to B could take 70 steps -- in which case you might not choose the right starting points to begin with. But this would probably only happen if there was something like a maze next to a normal neighborhood.

3. What's the relationship between trip distance and route complexity?

The graph above plots route distance (measured as the surface distance between the two lat-long pairs) against step counts. Aside from a few outliers, you'll notice that a really wide range of step counts is covered by a relatively narrow range of distances: that is, most of the variation in step counts is accounted for in trips less than a few hundred miles; and at the margin, an extra mile buys you very little in terms of route complexity.

Perhaps the most interesting points are those short routes with a large number of steps. See, for example, the 69-step route called out above (just over 1,000 miles), or the 67-step route from South Lyndeborough, NH to Hartley, GA (875 miles).

(You'll notice a few routes with more than 70 steps -- these can be safely ignored, since they either originate from or end up in Alaska (oops!)).

4. Can you generate a "heat map" that shades regions by their "coefficient of friction," i.e., a numerical estimate of how hard it is to drive through a particular region based on how many steps there are, on average, in a route passing through it?

This is left as an exercise for the reader, as is the task of finding even longer routes (here's a 75-stepper) and the more general underlying problem of understanding which features -- of cities and roads and geography -- are implicated in route complexity.

In the January 1983 volume of the journal Analysis, Gregory Kavka presented the following philosophical thought experiment:

An eccentric billionaire places before you a vial of toxin that, if you drink it, will make you painfully ill for a day, but will not threaten your life or have any lasting effects. The billionaire will pay you one million dollars tomorrow morning if, at midnight tonight, you intend to drink the toxin tomorrow afternoon. He emphasizes that you need not drink the toxin to receive the money; in fact, the money will already be in your bank account hours before the time for drinking it arrives, if you succeed. All you have to do is... intend at midnight tonight to drink the stuff tomorrow afternoon. You are perfectly free to change your mind after receiving the money and not drink the toxin.

It's probably worth asking why this is considered an interesting problem in the first place, since on face there might not seem to be anything difficult going on.

But Kavka seems to think that it would actually be very hard, if not impossible, for someone to intend at midnight tonight to drink a painful poison tomorrow if they knew that they could eventually back out without losing any money. In asserting this he is really taking two steps: first, to argue that a person would never actually drink the poison, because by the time they reach the moment of truth, the prize will have already been won or lost---and no one would choose pain vs. not-pain if all else is equal; and second, to argue that if you knew that you weren't going to drink the poison tomorrow, there is no way you could intend to tonight.

The first step is fairly sound, although one can imagine challenging it in the following way: suppose that you had somehow managed, last night, to intend to drink the poison today---isn't there then a sense in which you're committed to go through with it (such commitment being what initially enabled your intention)? If so, then it may be that to win the money you do have to drink the poison after all. (This was actually the tack taken by philosopher David Gauthier in a paper published shortly after Kavka's. See the Wikipedia page for more.)

It's an interesting possibility that cuts to the core of the problem: can someone intend to drink the poison, and if so, what would such a person look like (epistemologically, psychologically)? Would they be somehow bound, Gauthier-style, to follow through, or is there a way to win the money without having to endure a day of pain?

I certainly don't think it would be the strangest thing to ever happen, and actually I could imagine a few concrete ways you might pull it off:

1. You could force yourself to literally forget about the option to back out tomorrow. I doubt I could do this, but there must be some people whose minds are sufficiently powerful (or broken) to selectively "delete" memories. (In which case they would in fact follow through and drink the poison, unless the billionaire reminded them that they had the option not to.)
2. More easily, you could construct for yourself a sort of conspiracy theory in which the billionaire is tricking you, and in which you'll have no choice but to drink the poison tomorrow. You could get yourself all riled up this way, momentarily terrified by the prospect, but gradually talk yourself down to the point of acquiescence---"there are no lasting effects; it'll only be painful for a day"---mentally preparing yourself so well to drink the poison that you essentially "forget" about backing out, since that option no longer seems real. This train of thought may sound bizarre, but I'd wager that every day all sorts of paranoid people immerse themselves in far more elaborate fantasies. (And the benefit of pulling this one off is that you would wake up the next day a million dollars richer and amazingly relieved the moment the billionaire let you go.)
3. You could be one of those thrill-seekers who thinks it would add to your stock of "life experience" to endure a temporary bout of intense pain. (In this case you probably would end up drinking the poison.)
4. Or you could, quite like a regular person, decide that you really want the million dollars and that you'd be willing to endure a day of pain for it. You might then set out to find some way to intend tonight to drink the poison tomorrow, even though you know in the back of your mind that you are very likely to back out. So for the next several hours you might fight yourself, trying hard as you can to eliminate these nagging thoughts of backing out, flitting back and forth between "totally committed" and "knowing full well I won't go through with it." You might even start to consider options like #1-3, but you'd probably dismiss them for being too weird or somehow infeasible. Then finally you'd hit on a brilliant idea: a contract! You have long been telling yourself that "my word is my bond," that you are trustworthy, that other people might renege or cave but that you always come through. You are certain that if you signed a contract with yourself you couldn't break it. And so you'd draw one up, sign it, and sleep comfortably, slightly nervous about the day of painful illness ahead, but pleased to know that you've got a million dollars in the bag. And it would probably be enough to net you the cash. (Of course odds are that the next day you'd go back on your word, but I imagine we all know a few people who really are so steadfast that they'd actually drink the poison.)

There are no doubt many more methods available. The key point is that human psychology is warpable enough to satisfy the billionaire's demands---this is, after all, the same psychology that can willingly kamikaze itself in the name of God or country, that is so often ruled by fear and insecurity, that regularly violates expected utility theory, and that acts, for the most part, as though it's not headed toward an infinite doom.

So the real puzzle here, in my mind, is why Kavka thought this was a "puzzle" at all.

"It turns out" became a favorite phrase of mine sometime in mid 2006, which, it turns out, was just about the time that I first started tearing through Paul Graham essays. Coincidence?

I think not. It's not that pg is a particularly heavy user of the phrase---I counted just 46 unique instances in a simple search of his site---but that he knows how to use it. He works it, gets mileage out of it, in a way that other writers don't.

That probably sounds like a compliment. But it turns out that "it turns out" does the sort of work, for a writer, that a writer should be doing himself. So to say that someone uses the phrase particularly well is really just an underhanded way of saying that they're particularly good at being lazy.

Let me explain what I mean.

Suppose that I walk into a new deli expecting to get a sandwich with roast beef, but that when I place my order, the person working the counter says that they don't have roast beef. If I were to relay this little disappointment to my friends, I might say, "You know that new deli on Fifth St.? It turns out they don't even have roast beef!"

Or suppose instead that I'm trying to describe a movie to a friend, and that this particular movie includes a striking plot twist. If I wanted to be dramatic about it, I might say "...and so they let him go, thinking nothing of it. But it turns out that he, this very guy that they just let go, was the killer all along."

So far so good. Now suppose, finally, that I'm a writer trying to make an argument, and that my argument critically depends on a bit of a tall claim, on the sort of claim that a lot of people might dismiss the first time they heard it. Suppose, for example, that I'm trying to convince my readers that Cambridge, Massachusetts is the intellectual capital of the world. As part of my argument I'd have to rule out every other city, including very plausible contenders like New York. To do so, I might try something like this:

When I moved to New York, I was very excited at first. It's an exciting place. So it took me quite a while to realize I just wasn't like the people there. I kept searching for the Cambridge of New York. It turned out it was way, way uptown: an hour uptown by air.

Wait a second: that's not an argument at all! It's a blind assertion based only on my own experience. The only reason that it might sort of work is that it's couched in the same tone of surprised discovery used in those two innocuous examples above---as though after lots of rigorous searching, and trying, and fighting to find in New York the stuff that makes Cambridge the intellectual capital, it simply turned out---in the way that a pie crust might turn out to be too crispy, or a chemical solution might turn out to be acidic---not to be there.

That's what I mean when I say that pg (who, by the way, actually wrote that passage about Cambridge and New York) "gets mileage" out of the phrase: he takes advantage of the fact that it so often accompanies real, simple, occasionally hard-won neutral observations.

In other words, because "it turns out" is the sort of phrase you would use to convey, for example, something unexpected about a phenomenon you've studied extensively---as in the scientist saying "...but the E. coli turned out to be totally resistant"---or some buried fact that you have recently discovered on behalf of your readers---as when the Malcolm Gladwells of the world say "...and it turns out all these experts have something in common: 10,000 hours of deliberate practice"---readers are trained, slowly but surely, to be disarmed by it. They learn to trust the writers who use the phrase, in large part because they come to associate it with that feeling of the author's own dispassionate surprise: "I, too, once believed X," the author says, "but whaddya know, X turns out to be false."

Readers are simply more willing to tolerate a lightspeed jump from belief X to belief Y if the writer himself (a) seems taken aback by it and (b) acts as if they had no say in the matter---as though the situation simply unfolded that way. Which is precisely what the phrase "it turns out" accomplishes, and why it's so useful in circumstances where you don't have any substantive path from X to Y. In that sense it's a kind of handy writerly shortcut or, as pg would probably put it, a hack.

A commenter on Why The Law wondered whether we can "have a society whose output has equivalent K-complexity as ours, but is generated from simpler rules"—in effect seeking the simplest legal system that can sustain something like the U.S. economy.

The idea reminded me of two papers—"Economic Production as Chemistry," by Padgett, Lee, and Collier (2003), and "Evolution of Cooperative Problem-Solving in an Artificial Economy," by Baum and Durdanovic (2000)—because in each, the authors are trying to develop a minimal model of fruitful markets: what are the necessary conditions for productive collaboration? Which treatments of property and compensation generate stability, and which degrade? Must agents be intelligent? Altruistic?

Hypercycles

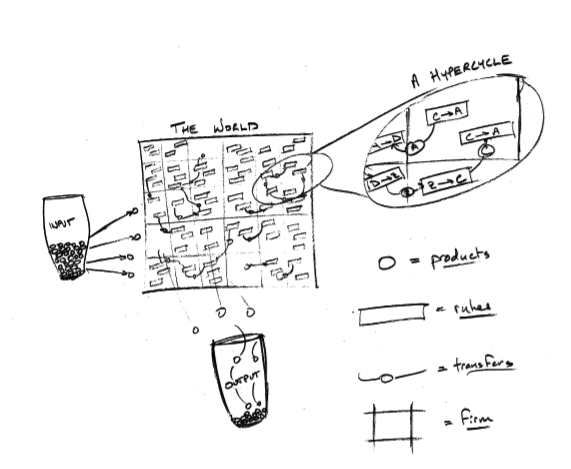
Padgett et al. imagine a grid-world with three basic components: firms, one in each cell, each of which has a random initial endowment of rules, which are simple procedures for transforming products. So for example the cell at (2, 3) may have a rule C -> F that takes the product C as input from one neighboring firm and spits out an F to another. It looks something like this:

A natural question to ask of such a world is whether it can sustain chain reactions, or coincidences where firm after firm spits out the very product that the next guy needs as input, as when a firm with rule A -> B happens to send off its B to a firm with rule B -> C.

In fact the model is deliberately set up with these chains in mind. Here are the rules of the game:

1. Initially, technologies are distributed randomly among the firms, which are arrayed on a large grid with wraparound—so that every firm, even if it's on an "edge," has eight potential trading partners.
2. In each "round" of the model (which proceeds in asynchronous discrete steps):
   • A random rule is chosen or "activated."
   • The firm that owns this rule grabs a product from its "input environment," modeled as an urn containing a bunch of products.
   • If the product it chooses is an input for the activated rule (e.g., if the product is a C and the rule is C -> Z), the rule does its thing and the output of its transformation is passed randomly onto one of the firm's neighboring trading partners.
   • Otherwise, the input product is sent to an output environment (also modeled as an urn).
3. The round's action continues as firms receive their neighbors' output. This step is important: if you've just successfully transformed A into Z, and pass the Z onto me, and I have a Z -> V rule, then we've just engaged in a "successful transaction."
4. Every time there is a successful transaction, one of the rules involved (in our example above, that would be one of A -> Z or Z -> V) is reproduced. It turns out that the behavior of the overall model depends a great deal on which one of the source or destination rules is copied. (See below.)
5. To encourage competition, every time one rule is reproduced, another one, chosen randomly, is killed off. So the total number of rules in play is held constant. This selection pressure, combined with the ability for rules to reproduce, is what keeps the world from degrading into an unproductive mess. (Again, more on this below.)
6. Firms that run out of rules die or "go bankrupt." Products sent their way are immediately directed to the output environment.
7. Firms continue to pass products around until one of these lands on a firm that doesn't have any compatible rules (i.e., if a D shows up at a firm that only has Z -> F, E -> F, and C -> D). At that point, the product is ejected into the output urn and a new rule is randomly chosen, as in step 1. (Meanwhile, and here's the "asynchronous" part, other firms are passing around other products. So the whole model doesn't reset when a single chain comes to an end.)

So how does anything interesting happen in this world? How do firms even survive? The short answer is "loops":

In this model, the minimal requirement for long-term survival, both of firms and of clusters, is to participate in at least one spatially distributed production chain that closes in on itself, to form a loop. Not all production chains within a trading cluster need be closed into loops. And more than one loop within a cluster is possible, in which case we may have a dense hypercyclic network of spatially distributed production rules. But loops within distributed chains of skill are crucial, not for production itself, but for the competitive reproduction of skills. Loops set up positive feedbacks of growth in skills that give firms that participate in them the reproductive ability to out-produce firms that do not. Put another way, clusters of firms can produce products with or without hypercycles, but firms whose skill sets participate in production chains that include loops have the further capacity to keep renewing each other through time. This is the chemical definition of life.

So the key is to promote these stable hypercycles. And it turns out that for loop maintenance, the model's most important ingredient is one touched on in step #4 above—the choice between "source" and "target" reproduction:

In the spatial topology setting, there are two variants of “learning by doing” that can and will be explored:

• “Source reproduction” is where the originating rule in a successful transaction is reproduced.
• “Target reproduction” is where the receiving rule in a successful transaction is reproduced.

For example, if A -> B receives an A from the input environment, transforms it into a B, and then successfully passes that B onto a neighboring B -> C, who transforms it again, then “source reproduction” is where the initiating A -> B reproduces, and “target reproduction” is where the recipient B -> C reproduces. Variation in mode of reproduction thus defines who benefits from the transaction.

We think of source reproduction as “selfish learning,” because the initiator of the successful transaction reaps the reward (like a teacher). And we think of target reproduction as “altruistic learning,” because the recipient of the successful transaction reaps the reward (like a student).

So which works better?

...in comparison with source reproduction, target reproduction dramatically increases the likelihood of growing stable hypercycles. And it also increases the spatial extensiveness and complexity of the firm cluster that hypercycles produce.

And why?

As explained in Padgett (1997), the basic reason for this superiority of target reproduction, or altruistic learning, is repair. Target reproduction combats dynamic instability in a way that source reproduction does not. The basic process of dynamic instability, causing hypercycles to crash, is that as one skill reproduces rapidly, under competition other skills are driven to zero, thereby breaking the reproductive loop of skills. Spatial topology distributes this dynamic into an overlapping series of neighborhoods, thereby inducing local heterogeneity. This opens the door for localized co-adaptive feedbacks to operate. But source reproduction, or selfish learning, does not really attack the basic dynamic instability itself. Source reproduction is this: an initial activated rule passes on its transformed product to a neighboring compatible rule, causing the original activated rule to reproduce. Under source reproduction, frequently activated rules reproduce more frequently, often eventually driving out of business even compatible neighbors on whom they depend for their own survival. As we shall see in the next section, other factors like endogenous environment can sometimes moderate this destructive dynamic, but source reproduction in and of itself does not eliminate the non-spatial instability problem.

In contrast, target reproduction is this: an initial activated rule passes on its transformed product to a neighboring compatible rule, causing the recipient rule to reproduce. Here the more frequently the initial rule is activated the more frequently the second recipient rule reproduces. In this way, a hypercycle can repair itself: as the volume of one skill in a loop gets low, high volumes of compatible skills in neighboring firms reach in to that low-volume skill to build it back up. Peaks and valleys along loops are smoothed.

To help get a grip on this distinction, it's worth asking whether there are any real-world examples of "altruistic reproduction." These would be domains in which the output of "upstream" firms promotes the growth of other firms down the line, thereby creating a rich self-sustaining production chain.

This seems true of many industries but especially true of information technology, where small software companies create huge markets (for themselves and others) by developing cheap, portable code for large enterprises. Even open source components—like Linux or MySQL—accelerate industry growth and feed opportunities back to software providers in the form of support contracts and custom coding projects. The result is symbiotic.

(In contrast, one could imagine how—in the kind of closed world explored in this paper—the success of something like a casino would have the perverse effect of draining its own lifeblood, by siphoning the bankrolls of active gamblers. In that way it could be construed as an example of "selfish (source) reproduction.")

The Hayek Machine

The immediate goal of Baum et al. is to find a way to solve computational problems with large state spaces, like a Rubik's cube. Their approach is to kickstart an economy of modules—little bits of computer code—that dynamically combine into complicated chains. If these chains were somehow arranged to exploit the structure of the problem at hand, the system would be able to limit its search to a tiny fraction of the space of possible moves.

Intelligent computation of that sort is easier said than done, and so most of the paper is devoted to exploring precisely which features of the module "economy" improve performance, and why.

Before getting into that, though, it might help to explore the simplest of the three problems under attack, called "Blocks World." With that under our belt it should be easier to understand the model more generally.

An instance of Blocks World has four stacks (0, 1, 2, and 3) of colored blocks. The leftmost stack (0) is your template—you never move any of its blocks as you play. Instead, your goal is to rearrange the blocks in the other three stacks—with the important caveats that (a) you can only grab the topmost block off a given stack and (b) you can only pick one up at a time—until stack 1 matches the template.

Here's a picture:

The "Hayek" referred to in the caption is the name of the economics-inspired computer program developed in the paper. It is of course an homage to the great Austrian economist Friedrich von Hayek, and it works as follows:

1. The program is a collection of modules, or mini computer programs, each with an associated "wealth." The authors think of these modules as agents because they can interact with the world (the game).
2. "The system acts in a series of auctions. In each auction, each agent simulates the execution of its program on the current world and returns a nonnegative number. This number can be thought of as the agent's estimate of the value of the state its execution would reach. The agent bids an amount equal to the minimum of its wealth and the returned number. The solver with the highest bid wins the auction. It pays this bid to the winner of the previous auction, executes its actions on the current world, and collects any reward paid by the world, as well as the winning bid in the subsequent auction. Evolutionary pressure pushes agents to reach highly valued states and to bid accurately, lest they be outbid." (You might want to re-read the preceding paragraph a few times, until you get a handle on exactly how the auctions work. It's not complicated—it's just that there's a lot of procedure packed into a few tight sentences.)

3. "In each auction, each agent that has wealth more than a fixed sum 10W_init creates a new agent that is a mutation of itself. Like an investor, the creator endows its child with initial wealth W_init and takes a share of the child's profit. Typically we run with each agent paying one-tenth of its profit plus a small constant sum to its creator, but performance is little affected if this share is anywhere between 0 and .25. Each agent also pays resource tax proportional to the number of instructions it executes. This forces agent evolution to be sensitive to computational cost. Agents are removed if, and only if, their wealth falls below their initial capital, with any remaining wealth returned to their creator. Thus, the number of agents in the system varies, with agents remaining as long as they have been profitable.

   "This structure of payments and capital allocations is based on simple principles (Baum, 1998). The system is set up so that everything is owned by some agent, interagent transactions are voluntary, and money is conserved in interagent transactions (i.e., what one pays, another receives) (Miller & Drexler, 1988). Under those conditions, if the agents are rational in that they choose to make only profitable transactions, a new agent can earn money only by increasing total payment to the system from the world. But irrational agents are exploited and go broke. In the limit, the only agents that survive are those that collaborate with others to extract money from the world.

   "When not everything is owned, or money is not conserved, or property rights are not enforced, agents can earn money while harming the system, even if other agents maximize their profits. The overall problem, then, cannot be factored because a local optimum of the system will not be a local optimum of the individual agents" [emphasis in original].

What happens when this system is let loose on Blocks World?

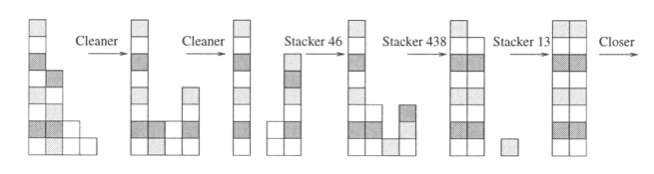
The population contains 1000 or more agents, each of which bids according to a complex S-expression that can be understood, using Maple, to be effectively equal to A * NumCorrect + B, where A and B are complex S-expressions that vary across agents but evaluate, approximately, to constants. The agents come in three recognizable types. A few, which we call "cleaners," unstack several blocks from stack 1, stacking them elsewhere, and have a positive constant B. The vast majority (about 1000), which we call "stackers," have similar positive A values to each other, small or negative B, and shuffle blocks around on stacks 2 and 3, and stack several blocks on stack 1. "Closers" bid similarly to stackers but with a slightly more positive B, and say Done.

At the beginning of each instance, blocks are stacked randomly. Thus, stack 1 contains about n/3 blocks, and one of its lower blocks is incorrect. All agents bid low since NumCorrect is small, and a cleaner whose B is positive thus wins the auction and clears some blocks. This repeats for several auctions until the incorrect blocks are cleared. Then a stacker typically wins the next auction. Since there are hundreds of stackers, each exploring a different stacking, usually at least one succeeds in adding correct blocks. Since bids are proportional to NumCorrect, the stacker that most increases NumCorrect wins the auction. This repeats until all blocks are correctly stacked on stack 1. Then a closer wins, either because of its higher B or because all other agents act to decrease the number of blocks on stack 1 and thereby reduce NumCorrect. The instance ends successfully when this closer says Done. A schematic of this procedure is shown in Figure 3 [below].

This NumCorrect that they keep referring to is a hand-coded module that counts the number of blocks in stack 1 (contiguous from the bottom up) that match the template. It's a good proxy for performance, and the measure is critical in helping the agents to know whether they're contributing value to the world (i.e., whether the program is on its way toward a solution).

If NumCorrect is left out of the system, then, performance degrades. Although it's possible for Hayek to evolve its own quick-and-dirty version, with this mere approximation it's only able to solve instances about 1/4 of the size as when NumCorrect comes hand-coded.

It's worth asking, then: how does code, be it NumCorrect or something simpler like Grab(i,j), "evolve" in the first place?

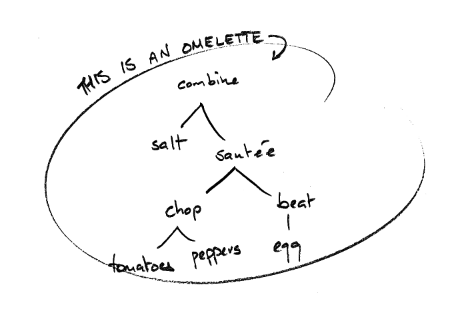
Agents are composed of S-expressions, or recursively-built trees of procedures. You can think of these as sort of like recipes:

The difference here, of course, is that whereas in the Recipe World you might have "sautée" or "chop," in Blocks World you have things like "grab" or "drop" or "look":

Our S-expressions are built out of constants, arithmetic functions, conditional tests, loop controls, and four interface functions: Look(i,j), which returns the color of the block at location i, j., Grab(i) and Drop(i), which act on stack i; and Done, which ends the instance. Some experiments also contain the function NumCorrect, and some contain a random node R(i, j), which simply executes branch i with probability 1/2 and j with probability 1/2. [This last randomizer function has the effect of "smoothing" the fitness landscape.]

All our expressions are typed, taking either integer, void, color, or boolean values. All operations respect types so that colors are never compared to integers, for example. The use of typing semantically constrains mutations and thus improves the likelihood of randomly generating meaningful and useful expressions.

It's hard to overstate how cool this process is. Out of a soup of random S-expressions—primitive codelets like adders and subtracters, if...then statements, loops, and "look" / "grab" / "drop" modules—it's possible for coherent strategical "agents" to evolve. On its own this idea is incredibly powerful: one can imagine all sorts of programs being developed automatically in this way, growing increasingly powerful by mutating and recombining useful snippets of code. Indeed, there's a whole field devoted to this approach to programming.

But what's even more spectacular is that these evolved computational lifeforms (of a sort) cooperate—via the auction process—in long computational chains, even when this requires that the initiating agents defer their rewards.

This last point is critical. It's not always obvious what the game's next best move may be, and often moves that are in the interest of long-term progress are (or look) counterproductive in the short term—as when you throw a bunch of incorrect blocks onto stack 1 to fish out an important block on stack 2. So it becomes basically impossible to solve any but the easiest Blocks World instances without the ability to "delay gratification," that is, to link up lots of low-or-no-reward-actions into chains that collectively work toward some bigger reward at their end.

The only way for this to work is to enforce the rules specified earlier:

A program cannot hope to form long chains of agents unless conservation of money is imposed and property rights are enforced. To evolve a long chain, where the final agent achieves something in the world and is paid by the world, reward has to be pushed back up the long chain so that the first agents are compensated as well. But pushing money up a long chain will not succeed if money is being created or is leaking, or if agents can steal money or somehow act to exploit other agents. If money is leaking, the early agents will go broke. If money is being created or being stolen, the system will evolve in directions to exploit this rather than creating deep chains to solve the externally posed problems. Solving the world's problems is very hard, and an evolutionary program will always discover any loophole to earn money more simply. [Eric Baum, What is Thought, p. 246.]

That's also why it's so important for auction winners in this round to pay their bids to winners from the last round. That way, those agents who most help folks downstream are able to collect larger bid payments—which helps them reproduce and stay alive—and, if their work consistently leads to large rewards down the line, their downstream partners will also reproduce (having collected money from the world) and set up yet more collaboration. It's exactly the same principle that we saw in the hypercycles world.

Conclusion

To return to the comment that kicked off this whole discussion, it now seems clearer what sorts of laws one minimally needs to sustain a rich economy. The trick is to encourage long, dynamically stable collaborative chains, and to do so requires mechanisms for transferring the rewards of productive activity to everyone who contributed; otherwise, agents who make the kind of short-term sacrifices that fuel deep cooperation will die out, and only the shallowest computation (i.e., production) will be possible.

In the hypercycles model, this was achieved by connecting reproductive success to successful transactions. Target reproduction in particular ensures that successful firms don't "burn out" their own partners.

And in the Hayek machine, property rights and conservation of money ensure that (a) the only way to earn money oneself is to create wealth for the world and that (b) money trickles back along productive chains to every contributor. [1]

These, then, are the deep compuchemical reasons that such a substantial portion of the U.S. legal system is devoted to enforcing contracts and protecting property rights. Such laws are the bedrock of our—or any—economy.

Notes

[1] Although it may seem that in these models payments go in opposite directions, they actually don't—even under a regime of "target" reproduction, hypercycles loop back on themselves, which means that A's altruistic contribution to B's reproductive success ends up helping A in the end, precisely because the two are wound up in a circle. Target reproduction works better because it keeps such circles alive, and thus allows payments to continue flowing appropriately.

Yesterday a paper I was reading made reference to a "Galtonian composite photograph." From the context I had a vague idea of what the phrase referred to, but I wanted to learn more. So I:

1. Googled "Galton" and clicked on the first result, the Wikipedia page for Sir Francis Galton.
2. Searched the text there for "composite," which turned up the following:

   Galton also devised a technique called composite photography, described in detail in Inquiries in human faculty and its development...

3. Googled once again for "Inquiries in human faculty and its development" (no quotes), which turned up a complete Google Books entry.
4. Searched inside that text for "composite," and found, finally, "Appendix A.—Composite Portraiture," which contained everything I might want to know on the subject.

The whole process took about two minutes.

I couldn't help but wonder, though, what my search would have looked like forty years ago, long before the Internet and the proliferation of personal computers. How would I have traced a casual allusion to its source?

Step 1: Go to the library

Short of phoning a friend, there would have been no way to look something up without going to some sort of library. If I lived in the sticks, my best hope would have been a wealthy resident's set of encyclopedias or some sort of bookmobile—essentially a cart that hauled boxes of books around to small towns. For any remotely obscure topic, I would have been out of luck.

Step 2: Card catalogs and the metasearch

Once I got to my local library, probably funded by Carnegie, my first task would have been to figure out where to start looking. It's a process that has been mostly obviated by search engines, whose crawling and indexing and relevance rankings allow one to scour the whole world at once, without much regard to where the info comes from.

Back in the day, though, I would have had to start a sort of metasearch to find the right books, periodicals, journals, or microfilms in which to begin my actual search.

Luckily, by the 1960s these materials were indexed exhaustively in large card catalogs, which mapped author names, titles, subject headings, or keywords to the precise coordinates of actual items.

Not so luckily, I would have had to know some author name, title, subject heading, or keyword to look for. In the case of my query above, "Galtonian composite image," I would have had several plausible angles of attack: the name "Galton, Sir Francis," which if I didn't know, I could discover in an encyclopedia; the key words "composite image"; or the subject heading "photography."

But what if I had no context for my query? For example, what if I ran into a sentence like, "He resembled Little Chandler, if not in size then in stature"? Clearly this is a reference to some moderately famous person or character, but without more to go on, how could I figure out what to look for in the card catalog?

It depended. If I suspected that this was a real person, I could have searched the Encyclopedia Brittanica, something like the Dictionary of National Biography (for dead people), or a Who's Who (for living people). Once I found my man, I could pick up a biography or two.

Finding a fictional character would have been more difficult, but still possible. There was actually something called the "Cyclopedia of Fictional Characters," or I could have consulted the once-apparently-indispensable "Benet's Reader's Encyclopedia," which in addition to characters also catalogs author names, novels, stories, literary terms, etc. If I had gotten a handle on where my character first appeared, it would then have been a matter of picking up that particular book. Problem solved.

Unfortunately, it turns out that "Little Chandler" doesn't appear in any of these. Which means I would have had to either ask a librarian—who might have some tricks up his sleeve (Dewey, of the Decimal System, once said, "...the librarian must be the index of indexes")—or a very well-read friend, or maybe a professor of literature.

Step 3: The deep crazy world of indexes

Supposing I did have some success with the card catalog—as I would if I were searching for "Galtonian composite photography" instead of "Little Chandler"—I would now be sitting at a table with a large stack of reference works, regular books, a newspaper microfilm, and maybe a few journal indexes, which are like regular indexes, but span the full output of hundreds or thousands of journal issues.

Indexes, by the way, are curious things. They don't work the same way as Google's "index," which is, in technical parlance, really a concordance, because it maps every word to either a snippet or the full text of the page on which it originally appears. Concordances, because they are such a pain to compile by hand, were really only created for stuff like the Bible or the works of Shakespeare. (Example.)

Real indexes (don't say "indices") only contain a small, carefully chosen subset of all possible terms. They're put together by professional indexers who work for publishers on a contractual basis. (Some authors do write their own indexes, but this is apparently frowned upon by the American Society for Indexing and one of Kurt Vonnegut's characters).

Theirs is difficult work. Indexers must take care to use a controlled vocabulary, i.e., a set of canonical headings that "solve the problems of homographs, synonyms and polysemes by a bijection between concepts and authorized terms." The idea is to avoid multiple entries like "Cats, 50-62" and "Felines, 175-183", and to make sure not to confuse the two meanings of words like "pool" (think swimming and billiards).

They must compose a semantically sensible and reliable syndetic structure, which is the complex network of inter-index references ("See also...") that link related topics. It's important to avoid circularity (A -> B -> A) and to consistently connect semantically "close" entries (i.e., if "General Patton" points to "WWII", you probably also want "General MacArthur" to point there). To do so requires a fairly detailed understanding of the book and its subject matter: Which topics are related? Are these four ideas subunits of some general concept? Is X important enough to index?

Finally, good indexers have to put themselves in the reader's shoes. What sorts of things will someone new to the subject be looking for? If they want to know more about X, what word will pop into their head? Will they care to see the reference on p. 124, or is it too cursory to be included?

There are whole journals devoted to the subject. In fact, if you want to see a great index, presumably you couldn't do much better than the journal index for the journal Indexer. (Among other things, there is a section in each issue devoted to "praising" and "censuring" indexes found and submitted by readers. Down the rabbit hole...)

Step 4: Read, read, read

In any case, to return to my hypothetical 1960s search, I would now be (reverently) perusing the indexes of each item in my stack. I'd be looking for words like "Galton" and "composite," and I'd quickly skim the text of every reference until I found something promising. If yet more books were mentioned—or if I found some encouraging titles in a bibliography—I'd dig them up as well. My stack would slowly grow, and recede, and grow again, as I discarded dead ends and pursued new leads.

In contrast to how things work today, I wouldn't just be reading the stuff most directly relevant to my query. I'd be tempted by all sorts of tangents along the way: unusual or obscure topics, or hilariously terrible writing, or some new fantastic author I'd never yet encountered. In the search for truth I'd be taking the scenic route—longer, sure, but maybe more rewarding.